Getting started

Contents

• Creating a spotted star
• Gaia

Creating a spotted star

Suppose you’d like to estimate the stellar centroid jitter for a star with a spot. We begin by creating a Star object:

from mrspoc import Star
star = Star(u1=0.5, u2=0.2)

We’ve set the quadratic limb darkening parameters u1, u2 to be similar to the Sun in the optical.

Now let’s add a Spot to the spot list attribute Star.spots, which is placed half a stellar radius in the positive x-direction, with radius 10% of the radius of the star:

from mrspoc import Spot
spot = Spot(x=0.5, y=0, r=0.1, contrast=0.7)
star.spots.append(spot)

The spot contrast, set to 70% here, should be interpreted as the intensity of the atmosphere in the spot as a fraction of the flux in the quiescent photosphere.

We can print the apparent stellar centroid using the ~mrspoc.Star.center_of_light attribute:

>>> star.center_of_light  
(-0.0013829556756940378, 0.0)

The centroid is in the negative x direction since the spot is in the positive x direction. We can see what this star and spot configuration look like with the plot function:

star.plot(col_exaggerate=100)

(Source code, png, hires.png, pdf)

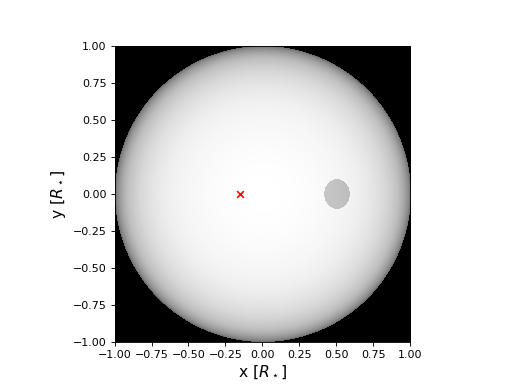
We’ve used the col_exaggerate keyword argument to exaggerate the centroid offset by a factor of 100, so we can see it.

Gaia

mrspoc has a few handy functions for computing Gaia’s expected astrometric precision, using the relations from Perryman et al. 2014.

You can predict the number of times Gaia will observe a given star with Nprime_fov, for a star at galactic latitude b:

>>> from mrspoc import Nprime_fov
>>> import astropy.units as u
>>> import numpy as np

>>> b = np.arange(0, 90, 10) * u.deg
>>> print(Nprime_fov(b)) 
[  51.9   53.7   58.5   69.1  107.4   85.    71.    65.2   62.8]

The results are non-integers because they are the mean number of visits for stars near each galactic latitude.

You can compute the galactic latitude b for a target given its SkyCoord like this:

>>> from astropy.coordinates import SkyCoord, Galactic
>>> import astropy.units as u
>>> from mrspoc import Nprime_fov

>>> coord = SkyCoord(ra=30*u.deg, dec=80*u.deg, frame='icrs')
>>> coord_gal = coord.transform_to(Galactic)
>>> print(coord_gal.b) 
17d32m24.9039s
>>> print(Nprime_fov(coord_gal.b))
55.6

You can compute the expected astrometric precision on a given target as a function of its Gaia bandpass G magnitude with sigma_fov, again taking from Perryman et al. 2014, this time from Equations 1-3:

>>> from mrspoc import sigma_fov
>>> sigma_fov(6.5)  
<Quantity 34.2301167881504 uarcsec>

>>> sigma_fov(15)  
<Quantity 81.99593485858512 uarcsec>